Preuve de l'exactitude de la conjecture des nombres premiers jumeaux (8ième problème de Hilbert)



Note à l'intention du lecteur

Le bref document qui suit se propose d'établir, à l'aide de moyens relativement simples, que la quantité de nombres premiers jumeaux est infinie, et donc que la conjecture qui concerne cette notion est en fait un théorème.
Les nombreuses études abordant cette question n'ont jamais abouti. Celle-ci se propose donc de mettre un terme définitif à ce problème. La méthode employée utilise seulement le principe d'inclusion-exclusion de De Moivre, le théorème de densité de Chebotarev, le troisième théorème de Mertens et quelques propriétés élémentaires d'arithmétique concernant la fonction indicatrice d'Euler.
Elle permet également de traiter, tout aussi efficacement, aussi bien la célèbre conjecture de Golback que celle de De Polignac dans des documents ultérieurs qui ne demandent plus, actuellement, que le temps de leur rédaction.

Ce document a été rédigé avec le plus grand soin et en ayant toujours présent à l'idée la maxime de Nicolas Boileau :
"Ce qui se conçoit bien s'énonce clairement et les mots pour le dire arrivent aisément".
Puisse le lecteur aborder ces lignes l'esprit ouvert et dénué de préjugés.

Avertissement
1.    Les deux nombres premiers 2 et 3, qui jouent souvent un rôle particulier et qui, ici, ne peuvent prétendre être des jumeaux, ont été rangés à part pour des raisons qui apparaîtront plus loin. Les complications qui en découlent sont assez minimes comme on pourra le voir et il en résultera seulement quelques restrictions faciles à comprendre.
2.    Lorsqu'il abordera la preuve du théorème qui fait l'objet de cette étude, ainsi que son corollaire, le lecteur ne devra jamais perdre de vue que la variable x (nombre entier) qui apparaît dans les "pseudo-égalités" a pour vocation de "tendre vers l'infini". Cela pour expliquer que, en de nombreux endroits, il n'est pas fait usage du signe = mais du signe ≈ . En effet, les deux membres des "pseudo-égalités" sont des quantités fluctuantes au gré de la variable mais qui ne sont jamais absolument égales : elles tendent seulement asymptotiquement l'une vers l'autre plus ou moins rapidement. Cette manière de faire, qui se comprend très bien, nous a paru plus simple que celle qui consisterait à introduire "lim" dans chacun des deux membres, ou à utiliser les notations de Landau pour être parfaitement rigoureux.
3.    Les mot "inférieur(s)" et "supérieur(s)" devront toujours être pris au sens large sauf spécification contraire.
4.    Pour simplifier l'écriture, nous admettrons que √x signifie, sans conséquence, aussi bien la racine exacte que sa partie entière (dans les applications numériques).
5.    Nous supposons connu du lecteur le fait que tout nombre premier est de la forme 6k-1 ou de la forme 6k+1

Soit x un entier naturel arbitraire, infiniment grand, mais parfaitement défini.

Considérons d'abord
l'ensemble M = {9, 15, 21, 25, 27, 33, 35, 39, 45, ...} ⊆ [9, x] des nombres impairs m non premiers, vérifiant 9 ≤ m ≤ x.
Cet ensemble peut être construit grâce au Crible de Sundaram présenté ci-dessous, ou à l'aide d'un programme informatique.

Cliquez sur le lien ci-dessous pour obtenir les 19867 premières valeurs de M (jusqu'à 49997 = (2×1190 + 1)(2×10 + 1)) et les 5133 premiers nombres premiers.

Veuillez cliquer

Ce crible (publié en 1934 par le mathématicien indien du même nom) permet de trouver les impairs non premiers grâce à des suites arithmétiques placées en lignes ou en colonnes.
Il utilise le fait qu'en déterminant l'ensemble des impairs composés, on peut en déduire l'ensemble des nombres premiers par complémentarité.
Considérons deux nombres impairs quelconques 2m + 1 et 2n + 1 (m et n différents de 0). On a : (2m + 1)(2n + 1) = 2(m + n + 2mn) + 1
Alors, en faisant varier m et n à partir de 1, on obtient l'ensemble des produits de deux nombres impairs, c'est-à-dire l'ensemble des impairs composés (non premiers) comme cela est partiellement reproduit dans le tableau ci-dessous où les lignes et les colonnes sont des suites arithmétiques ayant pour raison 4n+2 et 4m+2 respectivement.

Pour résumer, tout nombre impair (sauf 1) présent dans ce tableau est donc composé, tandis que tout nombre impair (sauf 1) absent de ce tableau est premier.

Crible de Sundaram
(ce n'est pas autre chose qu'une table de multiplication qui ne considère que les nombres impairs, mais voir la note 1)

Ligne rouge : valeurs de m        Ligne jaune : valeurs de 2m + 1
123456789101112...
35791113151719212325...
Colonne rouge :
valeurs de n



Colonne jaune :
valeurs de 2n + 1		 1391521273339455157636975 ...
25152535455565758595105115 125...
37213549637791105119133147161 175...
492745638199117135153171189207 225...
51133557799121143165187209231253 275...
613396591117143169195221247273299 325...
7154575105135165195225255285315345 375...
8175185119153187221255289323357391 425...
9195795133171209247285323361399437 475...
102163105147189231273315357399441 483525...
112369115161207253299345391437483529575...
122575125175225275325375425475525575625...
.............................................

Considérons ensuite,
d'une part l'ensemble M* = [11, 17, 23, 27, 29, 35, 37, 41, 47, ...} ⊆ [11, x+2] des nombres impairs m obtenus en ajoutant à chacun des éléments de M le nombre 2, donc vérifiant 11 ≤ m ≤ x+2,
et d'autre part la fonction f de M dans M* telle que, ∀m∈M    f(m) = m+2. Cette fonction est visiblement une bijection de M dans f(M) = M*. L'ensemble image f(M) = M* est la réunion de deux ensembles, visiblement non vides et évidemment disjoints : G0, ensemble des images qui ne sont pas des nombres premiers et G1, ensemble des images qui sont des nombres premiers.

Traduit autrement, ∀m∈ M
si f(m) ∈ G0, alors le couple (m, m+2) contient zéro nombre premier (ne contient aucun nombre premier) (d'où l'indice 0 pour G0),
si f(m) ∈ G1, alors le couple (m, m+2) contient (exactement) un nombre premier (d'où l'indice 1 pour G1) qui est m+2.

Considérons enfin
l'ensemble P = {5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, ...} des nombres premiers p vérifiant 5 ≤ p ≤ x+2 (2 et 3 étant donc rangés à part comme déjà signalé).
Evidemment, G1 est une partie de P et l'ensemble P-G1 n'est pas vide puisqu'il possède (entre autres) le nombre premier 5 qui n'appartient pas à G1 sinon 3 appartiendrait à M, ce qui est exclu.

Si p est un nombre premier de P-G1 supérieur à 13 et inférieur à x+2, alors, p-2 est forcément premier également puisque sinon, étant à la fois impair au même titre que p et composé, il serait dans M, et son image par f, c'est-à-dire p, serait dans M*, ce qui est impossible puisque p appartient à P-G1.

Essentiellement, il en résulte alors trois choses :
1) que p et p-2 sont en fait des nombres premiers jumeaux que nous désignerons respectivement par "sup-jumeaux" et "inf-jumeaux".
2) qu'ils sont respectivement de la forme 6k+1 et 6k-1 (k ≥ 2).
3) et que tous les couples de premiers jumeaux, sauf (3,5) et (5,7) s'obtiennent par le procédé indiqué

En outre, dans l'hypothèse précédente, puisque p-2 est de la forme 6k-1, alors, p-4, qui s'écrit 6k-3, étant visiblement un nombre impair, appartient à l'ensemble M.
La conséquence importante et immédiate est que p-2 est un élément de G1 lorsque p est un élément de P-G1 et que P-G1 contient tous les sup-jumeaux et rien d'autre.

On voit donc que tous les couples de nombres premiers jumeaux sont formés d'un premier p de P-G1 et du premier p-2 qui lui est associé dans G1,
ou si l'on préfère, d'un premier p de G1 et du premier p+2 qui lui est associé dans P-G1.
Nous pouvons observer au passage que les nombres premiers p de G1 autres que les inf-jumeaux sont ceux tels que p-2 et p+2 sont des impairs composés.

Le problème qui se pose donc pour commencer, afin d'établir que l'ensemble des premiers jumeaux est infini, est de dénombrer d'une manière aussi précise que possible cet ensemble P-G1, dénombrement qui ne semble pas, a priori, possible de manière directe, mais qui peut être obtenu en faisant la différence entre les cardinaux de P et de G1, puisque G1 ∪ (P-G1) = P et G1 ∩ (P-G1) = ∅
ce qui implique Card(G1) + Card(P-G1) = Card(P)

****

Arrivé à ce point, il semble bon d'illustrer les notions précédentes par un diagramme sagittal faisant ressortir la simplicité du cadre ainsi créé pour les besoins du raisonnement qui va suivre.

Afin de fixer les idées et à titre d'exemple, prenons pour p la valeur 13 appartenant à P-G1 (13 premier et impair, remarquons-le).
Alors p-2 (=11) est forcément premier, car, s'il ne l'était pas, étant impair au même titre que p (=13) et non premier, il appartiendrait à M, et son image p (=13) par f appartiendrait donc à M*
ce qui est visiblement contradictoire avec le fait qu'elle n'appartient pas à G1.

On voit alors clairement, dans le diagramme ci-dessus, que les couples de jumeaux sont formés
d'un nombre (l'inf-jumeaux) noir sur fond jaune dans G1, apparié avec un nombre (le sup-jumeaux) blanc sur fond rouge dans P-G1, comme (11 , 13) ; (17 , 19) ; etc ...

****

Une autre façon de présenter les choses consiste à mettre en regard, dans un tableau, les nombres impairs m non premiers de M et leurs images f(m) = m+2 dans M*, comme ci-dessous :

M     9   15   2125 27   33 35 39   45 49 51 55 57   63 65 69   75 77 81 85 87 91 93 95 99   105   111 115 117 119 121 etc...
    G0  ∪  G1  ∪  P-G1     5 7 11 13 17 19 23 27 29 31 35 37 41 43 47 51 53 57 59 61 65 67 71 73 77 79 83 87 89 93 95 97 101 103 107 109 113 117 119 121 123 etc...

Dans ce tableau,
1.    les cellules de la première rangée contiennent, sur fond blanc, les nombres impairs du crible de Sundaram et, sur fond noir, rien. C'est une manière de marquer que les nombres sur fond rouge de la deuxième rangée n'appartiennent pas à f(M)=M*;
2.    les cellules de la deuxième rangée contiennent sur fond blanc les éléments de   G0  , sur fond jaune ceux de   G1   (les uns étant les inf-jumeaux comme 11, 17, 29 et les autres non comme 23, 37, 47) et sur fond rouge ceux de   P-G1   (les sup-jumeaux)
En somme, on trouve les jumeaux dans les couples de cellules mitoyennes, celle de gauche étant jaune et celle de droite rouge.

On remarquera que :
1.    Le diagramme sagittal et le tableau contiennent forcément tous les nombres impairs (sauf 1 et 3).
2.    Tous les nombres premiers (sauf 2 et 3) étant de la forme 6k±1 (k>0), les inf-jumeaux, sauf 3, sont de la forme 6k-1 et les sup-jumeaux, sauf 5, sont de la forme 6k+1.
3.    Toute cellule de la seconde rangée, sur fond rouge (contenant un sup-jumeau sauf 5 et 7), est forcément précédée d'une cellule sur fond jaune (contenant un inf-jumeau).

****

Ainsi donc, la fonction f a permis de trier les nombres premiers et de séparer ceux qui sont des "sup-jumeaux" des autres.
Il est donc acquis, dorénavant, que les nombres de G1, qui sont tous premiers, ne peuvent être des "sup-jumeaux", et qu'en revanche, ceux de P-G1 sont tous des "sup-jumeaux" et qu'il ne peut y en avoir d'autres, les "inf-jumeaux étant, eux, dans G1, mélangés à d'autres premiers qui n'ont pas cette qualité.


Théorème
Soit R(x+2) le nombre de "sup-jumeaux" inférieurs à x+2;    R(√x+2) le nombre de "sup-jumeaux" inférieurs à √x+2;    γ = 0.5772156649 0153286060 la constante d'Euler-Mascheroni    et    C2 = 0.6601618158 4686957392 la constante de Shah et Wilson (constante des nombres premiers jumeaux).

Alors :




Démonstration

Désignons par R(x+2) (resp δ(x+2), n) le nombre de "sup-jumeaux" de [1, x+2] (resp. le nombre de premiers de G1, le nombre de premiers π(x+2) de [1, x+2]).
On a l'égalité : R(x+2) + δ(x+2) = π(x+2) - 2 = n - 2        (****)
la présence de -2 s'expliquant par le fait que les premiers 2 et 3, n'appartenant ni à P-G1 ni à G1, ne sont comptés ni dans R(x+2) ni dans δ(x+2), tandis qu'ils le sont dans π(x+2).

Le tableau suivant fait bien apparaître la justesse de la remarque précédente :

   x      x+2   les sup-jumeaux de [1, x+2]les premiers de G1R(x+2)δ(x+2)π(x+2)l'égalité
8105 ; 7 2042+0=4-2
18205 ; 7 ; 13 ; 1911 ; 174284+2=8-2
28305 ; 7 ; 13 ; 1911 ; 17 ; 23 ; 2944104+4=10-2
38405 ; 7 ; 13 ; 19 ; 3111 ; 17 ; 23 ; 29 ; 3755125+5=12-2
48505 ; 7 ; 13 ; 19 ; 31 ; 4311 ; 17 ; 23 ; 29 ; 37 ; 41 ; 4767156+7=15-2
58605 ; 7 ; 13 ; 19 ; 31 ; 4311 ; 17 ; 23 ; 29 ; 37 ; 41 ; 47 ; 53 ; 5969176+9=17-2
68705 ; 7 ; 13 ; 19 ; 31 ; 43 ;6111 ; 17 ; 23 ; 29 ; 37 ; 41 ; 47 ; 53 ; 59 ; 67710197+10=19-2
78805 ; 7 ; 13 ; 19 ; 31 ; 43 ; 61 ; 7311 ; 17 ; 23 ; 29 ; 37 ; 41 ; 47 ; 53 ; 59 ; 67 ; 71 ; 79812228+12=22-2
88905 ; 7 ; 13 ; 19 ; 31 ; 43 ; 61 ; 7311 ; 17 ; 23 ; 29 ; 37 ; 41 ; 47 ; 53 ; 59 ; 67 ; 71 ; 79 ; 83 ; 89814248+14=24-2
981005 ; 7 ; 13 ; 19 ; 31 ; 43 ; 61 ; 7311 ; 17 ; 23 ; 29 ; 37 ; 41 ; 47 ; 53 ; 59 ; 67 ; 71 ; 79 ; 83 ; 89 ; 97815258+15=25-2
........................

La présence de -2 dans la formule étant éclaircie, venons-en à la démonstration proprement dite du théorème.
Le but poursuivi est de trouver δ(x+2) pour en déduire R(x+2) à partir de l'égalité précédente, pour x infiniment grand.

Observons en premier lieu que chaque nombre m ∈ M (m impair non premier) est divisible par l'un, au moins, des premiers inférieurs à √m, nombre qui est lui-même inférieur ou égal à √x

Soit alors E = {3, 5, 7, 11, 13, 17, 19, 23, ... , pλ} l'ensemble des premiers pi (i ∈ [2, 3, ... , λ] p2=3; p3=5; p4=7; p5=11; ... etc ...) inférieurs à √x, autres que 2.
Tout nombre m de M a, au moins, un diviseur premier (qui ne peut être 2, m étant un composé impair) dans cet ensemble en vertu de la remarque précédente.

(A)
Considérons d'abord les suites arithmétiques Si ⊂ M formées des multiples inférieurs à x des différents premiers pi de cet ensemble E,
multiples obtenus en les multipliant exclusivement par les impairs strictement supérieurs à 1:

Les nombres envisagés sont donc tous de la forme (2k+3)pi      k∈N      et on a, l'expression ⌊ z ⌋ représentant la partie entière de z :

S2 = { 3×3,    5×3,    7×3,    9×3,    11×3,    13×3,     ... ,    ( 1 + 2 × ⌊(x - 3)/(2 × 3 )⌋ ) × 3 }
S3 = { 3×5,    5×5,    7×5,    9×5,    11×5,    13×5,     ... ,    ( 1 + 2 × ⌊(x - 5)/(2 × 5 )⌋ ) × 5 }
S4 = { 3×7,    5×7,    7×7,    9×7,    11×7,    13×7,     ... ,    ( 1 + 2 × ⌊(x - 7)/(2 × 7 )⌋ ) × 7 }
.......
et d'une manière générale :
Si = { 3pi,    5pi,    7pi,    9pi,    11pi,    13pi,     ... ,    ( 1 + 2 × ⌊(x - pi)/(2 × pi )⌋ ) × pi }

On remarquera trois choses à propos de ces suites arithmétiques :

1)    pi n'appartient pas à Si
2)    le premier nombre de Si est 3pi, le dernier est   ( 1 + 2 × ⌊(x - pi)/(2 × pi )⌋ ) × pi  
3)    la raison de Si est 2pi

Le tableau suivant, dans lequel les cellules en jaune ne sont là que pour faire le lien avec le crible de Sundaram et aussi pour justifier certaines remarques ultérieures, résume la situation.

 357 91113151719212325etc ...
3S291521273339455157636975etc ...
5S3152535455565758595105115125etc ...
7S4213549637791105119133147161175etc ...
11S533557799121143165187209231253275etc ...
13S6396591117143169195221247273299325etc ...
... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... Si ... ... ... ... ... ... ... ... ... ... ... ... etc ...

Ces suites, on le reconnait, ne contiennent pas autre chose que les nombres des lignes du crible de Sundaram présenté plus haut,
qui, dans la colonne jaune de gauche, contiennent un nombre premier, les autres lignes n'étant pas concernées.

Elles contiennent d'ailleurs, à l'évidence, et c'est ce qui fait leur intérêt, tous les nombres de ces autres lignes.

En d'autres termes :              (1)

(B)
Considérons ensuite les suites arithmétiques Si* ⊂ M* formées en ajoutant 2 à chacun des nombres des suites Si précédentes :
Les nombres envisagés sont donc tous de la forme (2k+3)pi+2      k∈N

Si* = { 3pi+2,    5pi+2,    7pi+2,    9pi+2,    11pi+2,    13pi+2,     ... ,    ( 1 + 2 × ⌊(x - pi)/(2 × pi⌋ ) × pi + 2 }

Ces suites arithmétiques particulièrement intéressantes sont présentées dans le tableau suivant et on remarquera aussi trois choses à leur propos :

1)    pi+2 n'appartient pas à Si*
2)    le premier nombre de Si* est 3pi+2, le dernier est   ( 1 + 2 × ⌊(x - pi)/(2 × pi )⌋ ) × pi + 2  
3)    la raison de Si* est 2pi comme pour Si

 357 91113151719212325etc ...
3S2*111723293541475359657177etc ...
5S3*172737475767778797107117127etc ...
7S4*233751657993107121135149163177etc ...
11S5*355779101123145167189211233255277etc ...
13S6*416793119145171197223249275301327etc ...
...... ... ... ... ... ... ... ... ... ... ... ... ... ...
...Si* ... ... ... ... ... ... ... ... ... ... ... ... etc ...

Il est clair, en vertu de l'égalité (1), que :               (2)

et donc que le nombre de premiers de G1, c'est-à-dire δ(x+2), (égal au nombre de premiers de M*) est égal au nombre de premiers de la réunion des suites Si*


Attention !
Le programme ci-dessous sera très utile
aux lecteurs courageux qui étudieront de près la
    note no 2

Dans le champ de gauche, saisissez un nombre compris au sens large entre 9 et 6240
puis cliquez sur le bouton pour afficher les suites Si et Si*



Or, nous avons, d'une part, le moyen d'évaluer le nombre de premiers de chacune des suites arithmétiques Si*, et, d'autre part, le moyen de cumuler les résultats obtenus sans doublons, avec une précision maximale à l'infini : il s'agit du théorème de densité de Chebotarev, d'une part, et du principe d'inclusion-exclusion de De Moivre, d'autre part.

Pour rappel, voici quelques résultats connus concernant certaines espèces de suites arithmétiques comme celles que nous rencontrons ici :


        Le théorème de la progression arithmétique de Dirichlet, généralisé par Chebotarev, affirme que, si a et b (a, b >0) sont deux nombres premiers entre eux,
alors il y a une infinité de nombres premiers parmi les termes de la progression arithmétique de terme général a + kb (k ∈ N et a ⋏ b = 1)

**********

Quelques valeurs de φ(n)
 0123456789
0 112242646
141041268816618
2812102282012181228
38301620162412361824
416401242202422461642
520322452184024362858
616603036324820663244
724702472364036602478
832544082246442564088
924724460467232964260

Calculette       n =                φ(n) =  
**********

        Le théorème des nombres premiers affirme, quant à lui, que, si π(n) est la suite dont le nième terme est égal au nombre de nombres premiers inférieurs à n,
alors cette suite tend asymptotiquement vers la suite n / ln(n), ce qui équivaut à dire que la suite différence de ces deux suites tend vers 0, ce qui s'écrit :

**********

        Enfin, la version quantitative du théorème de Dirichlet, démontrée en 1896 indépendamment par Hadamard et La Vallée Poussin, affirme que
le nombre π(n, a, b) de nombres premiers inférieurs à n au sens large dans la suite de terme général a + kb (k ∈ N et a ⋏ b = 1) est équivalent à Li(n)/φ(b).
Ce théorème est une généralisation du précédent qui correspond au cas a = 0 et b = 1.
Voir le tableau de la note no 7

Calcul de la valeur de li(x)

         

Arrivé à ce point, et pour la suite du raisonnement, le lecteur doit prendre conscience de la différence importante qui existe entre les suites Si et les suites Si*,
donc que, lorsque x tend vers l'infini, le théorème de Chebotarev s'applique parfaitement aux secondes, alors que ce n'est pas le cas pour les premières.
En effet, comme nous allons le voir,
le premier terme des suites Si* est premier avec la raison, contrairement à ce qui a lieu, de manière évidente, pour les suites Si, et c'est là toute la différence.

En effet, donc :
1.  Lorsque x tend vers l'infini, il en est de même de √x et donc du nombre de termes ⌊(x-pi)/2pi⌋ des suites Si*, puisque
     pi ≤ √x entraine ⌊(x-pi)/2pi⌋ = ⌊x/2pi-1/2⌋ ≥ ⌊x/2pi⌋ - 1 ≥ ⌊√x/2⌋ - 1.
     Le nombre des termes des suites Si* tend donc vers l'infini en même temps que x.
2.  Les premiers nombres de ces suites Si*, nombres que l'on pourrait désigner comme étant leurs "germes", sont de la forme 3pi+2,
     tandis que la raison est 2pi. Ces "germes" 3pi+2 sont premiers avec la raison 2pi.

Il s'agit d'établir que 3pi+2 et 2pi sont premiers entre-eux du fait que pi est impair :
Si d∈N est un diviseur commun de pi+2 et de 2pi, alors, ∃r∈N et ∃s∈N tels que pi+2=dr et 2pi=ds.
On en déduit ds+4=2dr donc 2dr-ds=d(2r-s)=4 et il en résulte que d ne peut prendre que les valeurs 1, 2 ou 4.
Les valeurs 2 et 4 étant exclues (puisque sinon d, pair, diviserait le nombre impair pi+2 ce qui est impossible), on en déduit que d=1 et que pi+2 et 2pi sont bien premiers entre-eux.
En conséquence de quoi 3pi+2 et 2pi sont également premiers entre-eux car si d divise ces deux nombres, il divise à la fois 2pi et leur différence pi+2 ce qui implique d=1 d'après ce qui précède
(cela n'a rien d'étonnant puisque si a est premier avec b, il est aussi premier avec a+b et a-b et réciproquement).

Nous allons donc pouvoir appliquer le théorème de densité de Chebotarev non seulement à chaque suite Si* mais aussi aux intersections de ces suites prises 2 à 2, 3 à 3, etc..., comme on va le voir.

**********

λ étant l'indice du nombre premier immédiatement inférieur à √x ,  𝓅 la fonction retournant le nombre de premiers d'un ensemble d'entiers et φ la fonction indicatrice d'Euler, on a successivement :


On peut être étonné de voir apparaître le terme dans l'égalité ci-dessus.
Pourtant, sa présence s'explique du fait que, dans chacune des suites Si* considérées dans le calcul, les sup-jumeaux pi+2 n'ont pas lieu d'être comptabilisés (alors qu'ils le seraient) puisqu'ils ne font pas partie des suites Si* comme on l'a vu.
Ainsi, les sup-jumeaux 5, 7 et 13 par exemple, auraient été pris en compte dans le calcul, à tort, puisqu'en fait ils ne font pas partie des suites
S2*, S3* et S5*.
Le nombre total des sup-jumeaux de cette espèce étant R(√x + 2), ce nombre doit donc être retranché dans l'expression du nombre total
de sup-jumeaux inférieurs à x+2 que donne l'application judicieuse du théorème de Chebotarev.

Cette remarque faite, nous devons nous arrêter ici un instant pour justifier l'égalité qui suit.
En effet, il s'agit, à partir de maintenant, d'évaluer, à l'aide du théorème de densité de Chebotarev, les nombres sous les Σ,
et nous devons donc prouver, au préalable, que les conditions d'application de ce théorème sont bien satisfaites.

Nous avons déjà prouvé que le dit théorème s'applique aux suites Si*, mais qu'en est-il de leurs intersections 2 à 2, 3 à 3, etc... ?
Occupons-nous donc, pour commencer, des intersections de la forme Si ∩ Sj, et rappelons nous
d'une part que les nombres des suites Si sont de la forme (2k+3)pi (k∈N) et donc que ceux des suites Si* sont de la forme (2k+3)pi + 2 (k∈N)
et d'autre part que ces suites ont pour raison 2pi l'une et l'autre par construction.

Les éléments communs à Si et Sj étant les multiples à la fois de pi et de pj, ces éléments communs sont donc les multiples de pipj puisque pi et pj sont premiers, donc premiers entre-eux.
Il en résulte que les intersections Si ∩ Sj sont évidemment des suites arithmétiques dont le premier terme est 3pipj et la raison 2pipj
D'où il découle que les intersections Si* ∩ Sj* sont aussi des suites arithmétiques dont le premier terme est 3pipj+2 et la raison 2pipj.

Il ne reste plus à montrer que 3pipj+2 et 2pipj sont premiers entre-eux du fait que pipj est impair :
Si d est un diviseur commun de pipj+2 et 2pipj, alors, ∃r∈N et ∃s∈N tels que pipj+2=dr et 2pipj=ds.
On en déduit 2pipj+4=ds+4=2dr donc 4=2dr-ds=d(2r-s) et il en résulte que d ne peut prendre que les valeurs 1, 2 ou 4.
Les valeurs 2 et 4 étant exclues (puisque sinon d, pair, diviserait le nombre impair pipj+2 ce qui est impossible), on en déduit que d=1 et que pipj+2 et 2pipj sont bien premiers entre-eux.
En conséquence de quoi 3pipj+2 et 2pipj sont également premiers entre-eux car si d divise ces deux nombres, il divise à la fois 2pipj et leur différence pipj+2 ce qui implique d=1 d'après ce qui précède.

Les résultats précédents s'étendent sans difficulté aux intersections de plus de trois suites Si* et s'établissent de la même manière :
par exemple, Si* ∩ Sj* ∩ Sk* est la suite arithmétique qui a pour premier terme 3pipjpk+2 et pour raison 2pipjpk et là encore 3pipjpk+2 et 2pipjpk sont premiers entre-eux.

Ainsi, étant assurés de pouvoir appliquer le théorème de densité de Chebotarev aux expressions figurant sous les Σ dans l'égalité précédente,
nous avons, pour x infiniment grand (condition d'application du théorème) :


Eu égard aux questions que le lecteur peut être amené à se poser,
nous invitons ici celui qui aura pris connaissance des pseudo-égalités ci-dessous
à lire attentivement les remarques développées dans la note no 2

Cliquer ici pour y accéder


Et puisque 2 et les pi sont premiers donc premiers 2 à 2, en tenant compte du fait que φ(2)=1 on a, en vertu d'une propriété élémentaire de l'indicatrice :

Cela dit, la dernière égalité devient (voir la note 3) :

et enfin, puisque pi est premier ∀i, (ce qui entraîne φ(pi)=pi-1) :

L'égalité (****) ci-dessus R(x+2) + δ(x+2) = π(x+2) - 2 = n - 2, qui s'écrit encore : R(x+2) + 𝓅(M*) = π(x+2) - 2 = n - 2, jointe à la précédente donne donc pour x infiniment grand :

c'est-à-dire :

Nous allons, dans ce qui suit, utiliser le troisième théorème de Mertens et la constante de Shah et Wilson (constante des nombres premiers jumeaux) pour évaluer le dernier second membre.

Rappelons que ce troisième théorème de Mertens affirme en substance que, si un entier y tend vers l'infini et si p est un nombre premier inférieur à y, alors, γ étant la constante d'Euler-Mascheroni :

    ce qui s'écrit encore :    

Si on donne à y la valeur √x, et si on élimine le nombre premier 2 dans ce produit faisant intervenir tous les nombres premiers inférieurs à y, cette égalité devient :

Mais alors, si l'on remarque que la constante C2 des nombres premiers jumeaux, s'écrit :

on peut lui donner la forme ci-dessous faisant intervenir l'égalité de Mertens :

On a donc :

    d'où :    

et enfin, (ce que nous devions établir) :

La pseudo égalité précédente peut encore s'écrire :

Sous cette forme, ce résultat montre deux choses :
1) que le nombre de sup-jumeaux est infini
2) pourquoi il y a toujours des sup-jumeaux dans l'intervalle [√x+2, x+2]

Le dernier membre de cette égalité étant lentement croissant, on comprend aussi pourquoi les nombres premiers jumeaux se raréfient au fur et à mesure que x croît,
et pourquoi ils sont cependant en nombre infini.

Note
Si l'on remplace dans la pseudo égalité ci-dessus x par 22k, autrement dit si l'on prend comme variable l'entier k, cette pseudo égalité devient :

En outre, puisque,
1) les nombres envisagés sont très grands, ce qu'il ne faut pas oublier ni perdre de vue,
2) il s'agit d'ordre de grandeur, ce qui autorise à négliger dans ces égalités les nombres 2 sans nuire au résultat,

on obtient l'écriture simplifiée très significative :

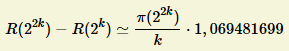
Mieux encore, puisque R(2k) est de plus en plus négligeable devant R(22k) au fur et à mesure de la croissance de k, et que la constante 1,069481699 ne change guère les résultats :

En posant x = 2k, c'est-à-dire k = ln(x)/ln(2), on a alors :

Cette formule, ici établie, est en somme analogue à la pseudo-égalité affichée en rouge ci-dessous, résultant de la conjecture connue qui, dès lors, serait établie :

    (Hardy-Littlewood)

Appliqués à de grands nombres, leurs résultats sont très sensiblement les mêmes puisque le dénominateur ln(x) tend vers l'infini (bien que de plus en plus lentement) :
Pour que les deux formules soient identiques, il suffit de remplacer ln(4) par ln(3.744633)

Les exemples numériques ci-dessous pour des valeurs de x croissantes semblent bien confirmer l'exactitude de ces formules :

 AB C D
xR(x)π(x)R(x)/π(x)ln(4)/ln(x)
1,3862944/ln(x)		A - B(A - B)/A2 × C2 × π(x)/x
1,3203236 × π(x)/x		A - C(A - C)/A2C2/ln(x)
103351680,2083330,2006870,0076460,03670,221814-0,0134810,06470,191136
10420512290,1668020,1505150,0162870,09760,1622680,0045340,02720,143352
105122495920,1276060,1204120,0071940,05640,1266450,0009610,00750,114682
1068169784980,1040660,1003430,0037230,03580,1036430,0004230,00400,095568
107589806645790,0887480,0860080,0027400,03090,0877460,0010020,01130,081916
5.10723910130011340,0796700,0782000,0014700,01840,0792490,0004210,00530,074479
10844031257614550,0764240,0752570,0011660,01530,0760700,0003540,00460,071676
1093424506508475340,0673480,0668950,0004530,00670,0671350,0002130,00310,063712
1010274126794550525110,0602470,0602060,0000410,00070,0600810,0001660,00270,057341
101122437604841180548130,0544860,054733-0,0002470,00450,0543720,0001140,00210,052128
10121870585220376079120180,0497390,050172-0,0004330,00870,0496550,0000840,00170,047784
1013158346648723460655368390,0457560,046312-0,0005560,01210,0456920,0000640,00140,044108
101413578032166532049417508020,0423660,043004-0,0006380,01500,0422320,0001340,00300,04058
10151177209242304298445704226690,0394440,040137-0,0006930,01750,0394040,0000400,00100,038227
1016103041956972982792383410339250,0369010,037629-0,0007270,01970,0368680,0000330,00090,035838

On constate alors, sans pour autant en tirer des conclusions définitives, que :
1) la proportion des sup-jumeaux parmi les nombres premiers est de plus en plus faible.
2) les pseudo-égalités semblent d'autant mieux réalisées que x est plus grand.
3) sauf pour la première rangée, C est toujours inférieur à A, ce qui n'est pas le cas pour B.


Corollaire
Avec les notations précédentes, on peut dire qu'il existe une constante ʋ telle que, ∀x
donc en particulier lorsque x tend vers l'infini :




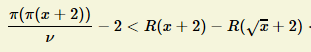
Preuve

n étant toujours π(x+2) nous allons chercher un encadrement de 1/kk', k et k' étant définis par :

Pour x grand, on a : n2 = [π(x+2)]2 ≈ (x+2)×{(x+2)/[ln(x+2)]2}

Or, pour x > 11, l'expression (x+2)/[ln(x+2)]2 a pour valeur un nombre strictement supérieur à 2 et croît rapidement avec x.
(à titre d'exemple, pour x + 2 = 1000, 2000, 20000, 100000, 1000000, 10000000, ce quotient a pour valeur respectivement 20, 34, 203, 754, 5239, 38492)
On peut donc affirmer, sans risque de se tromper, que, pour x > 11, et à plus forte raison pour x grand, n2 > x+2 > x.(cette inégalité est même valable dès que x > 2)
Pour un nombre x strictement supérieur à 3, on a donc n < x < n2 et donc ln(n) < ln(x) < 2 ln(n) ou 1 < ln(x)/ln(n) < 2. Donc   k ∈ ]1; 2[  .

D'autre part, toutes les études antérieures menées sur le comportement asymptotique de k' montrent que :

On a donc k' ∈ ]1; 1,25506[ et il en résulte l'encadrement de 1/kk' :

D'où l'on déduit successivement, puisque, x étant grand et   π(n)/kk' = n/ln(x)  , les détails du calcul faisant intervenir le résultat du théorème étant laissés au lecteur :

Avec les valeurs connues : γ=0.57721566490, eγ=1.78107241799, e-γ=0.56145948356 et C2=0.66016181584 on obtient :

Ainsi, il existe bien une constante ʋ ≈ 1,693034 vérifiant l'énoncé ci-dessus.
La borne inférieure de la double inégalité est en soi une preuve de l'infinité des nombres premiers jumeaux, tandis que la borne supérieure renseigne sur leur raréfaction.

Remarques

(1)
La première inégalité peut être améliorée.
En effet, pour x supérieur ou égal à 121 (par exemple), on a R(√x + 2) > 2.
Donc - R(√x + 2) < -2 et donc R(x + 2) - R(√x + 2) < R(x + 2) - 2
Donc, à plus forte raison, lorsque x est très grand pour justifier le corollaire :

Ce qui autorise à écrire

(2)
Les inégalités précédentes ont été établies pour les valeurs de x vérifiant la condition la plus forte, à savoir x>17,
mais on peut vérifier facilement que la première inégalité est valable, en fait, quel que soit x et aussi que la seconde est valable pour x>8.
Cette remarque est évidemment sans conséquence pour le but poursuivi.

(3)
De tout ce qui précède on peut conclure en disant que, au voisinage de l'infini, il existe une quantité non négligeable de nombres premiers jumeaux dans l'intervalle [√x+2, x+2].

(4)
L'intervalle [√x+2, x+2] contient donc plus de sup-jumeaux que π(π(x+2))/1,693034
La densité de ces jumeaux dans cet intervalle pose dorénavant un problème comparable à celui de la densité des premiers dans l'intervalle [1, n], qui en possède π(n),
(objet du théorème des nombres premiers).


Note no 1

Le véritable crible de Sundaram n'est pas celui présenté en haut de cette page, mais le suivant :

 357911131517...
347101316192225...
5712172227323742...
71017243138455259...
91322314049586776...
111627384960718293...
1319324558718497110...
15223752678297112127...
172542597693110127144...
..............................

dans lequel les lignes et les colonnes sont des suites arithmétiques ayant pour raisons évidentes les nombres marqués dans les régions en jaune.
On peut montrer que si un nombre n se trouve dans ce tableau, alors 2n + 1 n'est pas premier et qu'à l'inverse, si un nombre n ne se trouve pas dans ce tableau, alors 2n + 1 est premier
ce qui peut se résumer en disant :
ou bien    n figure dans ce tableau si et seulement si 2n + 1 n'est pas premier
ou bien    n ne figure pas dans ce tableau si et seulement si 2n + 1 est premier.

Si on ajoute l'unité au contenu de chacune des cellules précédentes, on obtient le tableau :

358111417202326...
5813182328333843...
71118253239465360...
91423324150596877...
111728395061728394...
1320334659728598111...
15233853688398113128...
172643607794111128145...
..............................

On a alors la proposition suivante :
Un entier naturel n n'appartient à aucun de ces tableaux si et seulement si 2n - 1 et 2n + 1 sont des nombres premiers jumeaux.
En conséquence de quoi un naturel autre que 2 qui n'appartient à aucun de ces tableaux est un multiple de 3.


Note no 2

On objectera à juste titre que, parmi les sous-suites du type Si* ∩ Sj* ∩ Sk* ∩ ... ∩ ... ∩ Sλ*, formées, comme cela a été dit, avec les multiples impairs des produits pipjpk ... pλ ( i<j<k< ... <λ ), certaines d'entre-elles ne possèdent pas une infinité de termes (ce qui veut dire en fait ne possèdent pas un très grand nombre, mais nécessairement fini, de termes et même, peuvent être vides), et mettent ainsi en échec l'application qui est faite du théorème de Chebotarev qui ne concerne que des suites infinies, prises dans le sens précédent.

Il faut donc bien comprendre que le théorème de Chebotarev ne peut s'appliquer, c'est-à-dire ne peut donner lieu à l'écriture d'expressions utiles, desquelles on peut tirer des conclusions, que pour des suites finis, mais qui contiennent un très grand nombre de termes, car l'infini n'est pas accessible autrement que par ce procédé.

Les suites que nous qualifierons de défectueuses, qui donc contiennent trop peu de termes pour les raisons évoquées, ou qui, même, sont vides (ce seront les seules dont nous nous occuperons dans les exemples qui suivent) et qu'il faudrait rejeter, sont celles pour lesquelles les produits des différents nombres premiers pi qui concourent à leur formation sont peu éloignés de x
(et même supérieurs à x dans le cas des suites vides).

Cependant, si on applique le théorème de Chebotarev en tenant compte indûment de ces suites trop courtes, obtenues avec x grand, (nous devons constamment insister sur cet aspect), on ne modifie pas sensiblement le résultat que l'on obtiendrait en les éliminant puisque, lorsque x est grand et que le nombre de premiers considérés devient important, les indicatrices d'Euler de leurs différents produits (ou, si l'on préfère, ce qui est la même chose, les différents produits des indicatrices d'Euler de ces nombres premiers) placées aux dénominateurs deviennent absolument considérables devant n = π(x + 2) placé aux numérateurs, et ce phénomène va s'amplifiant au fur et à mesure que x croît, de sorte que ces termes en excédent tendent de plus en plus vite vers zéro quand x tend vers l'infini.
Autrement dit, les termes qui s'ajoutent et se retranchent indûment dans l'expression, et qui se compensent plus ou moins en raison de l'alternance des signes plus et moins, deviennent négligeables devant les autres termes significatifs, d'où il résulte que la "pseudo-égalité" ne perd rien de son sens puisqu'il n'est en rien question d'établir une égalité rigoureuse entre les deux termes de l'expression concernée.

On doit par ailleurs observer, ce qui n'est pas négligeable, loin de là, que, au fur et à mesure que x croît et donc que le nombre de facteurs des produits pipjpk ... pλ ( i<j<k< ... <λ ) engendrant les sous-suites Si* ∩ Sj* ∩ Sk* ∩ ... ∩ ... ∩ Sλ* augmente, ces produits prennent très rapidement des valeurs considérables dépassant très vite le nombre x.
Il faut donc admettre que le nombre des intersections Si* ∩ Sj* ∩ Sk* ∩ ... ∩ ... ∩ Sλ* contenant un nombre significativement grand d'éléments est relativement très faible en comparaison de la "dimension" de x, même pour des valeurs de x assez petites.


Afin de bien montrer l'importance des considérations précédentes, nous allons voir en détail ce qu'il en est par exemple dans le cas où x = 900, nombre qui n'est pas particulièrement grand

R(√900 + 2) = R(32) = 5
n = π(900 + 2) = 154
Il y a 9 nombres premiers inférieurs à √900 = 30, et ils sont : 3, 5, 7, 11, 13, 17, 19, 23, 29
Leur produit est égal à 3 234 846 615 (nombre très grand par rapport à 900, plus de 3 500 000 fois plus grand)
Par ailleurs, puisque : 3 × 5 × 7 × 11 = 1155 > 900, toutes les suites formées à partir des multiples impairs du produit de quatre et plus des nombres premiers précédents sont vides.
Il en est de même de certaines suites formées à partir des multiples impairs du produit de trois des nombres premiers précédents puisque 5 × 7 × 29 = 1015 > 900
Les valeurs de l'indicatrice d'Euler qui correspondent à ces premiers sont : φ(3) = 2, φ(5) = 4, φ(7) = 6, φ(11) = 10, φ(13) = 12, φ(17) = 16, φ(19) = 18, φ(23) = 22, φ(29) = 28
(rappelons que si α est un nombre premier, alors φ(α) = α - 1)

d'où la valeur de l'expression donnant approximativement le nombre de premiers de G1, valeur calculée en considérant les résultats de la note 3 :
- 5 + 154 × (1 - 1/2 × 3/4 × 5/6 × 9/10 × 11/12 × 15/16 × 17/18 × 21/22 × 27/28) = - 5 + 154 × (1 - 0.21011352539) = 116.6425
tandis que le nombre véritable de premiers de G1 est 152 - 35 = 117 (le nombre de premiers, sauf 2 et 3, inférieurs à 900 diminué du nombre de sup-jumeaux inférieurs à 900)
On remarquera que l'écart est cependant très faible entre ces deux résultats. Et pourtant :

Dans cet exemple, il y a en tout 511 suites possibles (somme des nombres de combinaisons 1 à 1, 2 à 2, ... , 9 à 9 des 9 nombres premiers, diminuée de l'unité, c'est-à dire 29 - 1 = 512 - 1 = 511)
Puisque 3 × 5 × 7 × 11 = 1155, toutes les suites formées à partir du produit de quatre ou plus de nombres premiers sont donc vides. Leur nombre est 382
Parmi les autres qui sont au nombre de 129 il ne s'en trouve que 35 qui ne sont pas vides.
Les 9 suites formées à partir d'un seul premier en font évidemment partie
Parmi les 36 suites formées à partir du produit de 2 premiers on en compte seulement 20
Parmi les 84 suites formées à partir du produit de 3 premiers on en compte seulement 6
Pour résumer, sur les 511 combinaisons possibles des 9 nombres premiers, il n'y a que 35 combinaisons qui engendrent des suites qui ne sont pas vides et parmi celles-ci, il s'en trouve encore qui n'ont que quelques éléments.

**********

Si l'on remplace 900 par 1600, les résultats sont les suivants :

R(√1600 + 2) = R(42) = 5
n = π(1600 + 2) = 252
Il y a 11 nombres premiers inférieurs à √1600 = 40, et ils sont : 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37
Leur produit est égal à 3 710 369 067 405 (nombre très grand par rapport à 1600, plus de 2 300 000 000 fois plus grand)
Par ailleurs, puisque : 3 × 5 × 7 × 11 × 13 = 15015 > 1600, toutes les suites formées à partir des multiples impairs du produit de cinq et plus des nombres premiers précédents sont vides.
Il en est de même de certaines suites formées à partir des multiples impairs du produit de quatre et même de trois des nombres premiers précédents puisque 3 × 5 × 7 × 17 = 1785 > 1600 et 3 × 17 × 37 = 1887 > 1600 respectivement
Les valeurs de l'indicatrice d'Euler qui correspondent à ces premiers sont : φ(3) = 2, φ(5) = 4, φ(7) = 6, φ(11) = 10, φ(13) = 12, φ(17) = 16, φ(19) = 18, φ(23) = 22, φ(29) = 28, φ(31) = 30, φ(37) = 36
(rappelons que si α est un nombre premier, alors φ(α) = α - 1)

d'où la valeur de l'expression donnant approximativement le nombre de premiers de G1, valeur calculée en considérant les résultats de la note 3 :
- 5 + 252 × (1 - 1/2 × 3/4 × 5/6 × 9/10 × 11/12 × 15/16 × 17/18 × 21/22 × 27/28 × 29/30 × 35/36) = - 5 + 252 × (1 - 0.197467803955) = 197.2381
tandis que le nombre véritable de premiers de G1 est 249 - 50 = 199 (le nombre de premiers, sauf 2 et 3, inférieurs à 1600, diminué du nombre de sup-jumeaux inférieurs à 1600)
On remarquera que l'écart est cependant très faible entre ces deux résultats. Et pourtant là encore :

Dans cet exemple, il y a en tout 2047 suites possibles (somme des nombres de combinaisons 1 à 1, 2 à 2, ... , 11 à 11 des 11 nombres premiers, diminuée de l'unité, c'est-à dire 211 - 1 = 2048 - 1 = 2047).
1924 sont vides (94%) et 123 seulement ne le sont pas (6%)
Voici, de façon détaillée, les résultats obtenus. En combinant les nombres premiers précédents :
1 à 1, on obtient 0 suite vide sur un total de 11.
2 à 2, on obtient 0 suite vide sur un total de 55.
3 à 3, on obtient 110 suites vides sur un total de 165.
4 à 4, on obtient 328 suites vides sur un total de 330.
5 à 5, on obtient 462 suites vides sur un total de 462.
6 à 6, on obtient 462 suites vides sur un total de 462.
7 à 7, on obtient 330 suites vides sur un total de 330.
8 à 8, on obtient 165 suites vides sur un total de 165.
9 à 9, on obtient 55 suites vides sur un total de 55.
10 à 10, on obtient 11 suites vides sur un total de 11.
11 à 11, on obtient 1 suite vide sur un total de 1.

Il semble donc que l'on soit en droit d'estimer, puisque ce phénomène ne peut que s'amplifier et bien que ce postulat ne soit pas établi à l'aide des méthodes mathématiques habituelles, que l'usage, quoique abusif, qui est fait ici du théorème de Chebotarev soit parfaitement justifié jusqu'à preuve du contraire.

**********
Afin de rendre ces remarques relativement évidentes, voyons sur des exemples comment se traduisent ces observations:
Prenons pour x une valeur quelconque de l'intervalle [121, 168[ , dont la racine carrée appartient à [11, 13[ ; par exemple 143 pour fixer les idées.
En s'aidant du programme proposé juste après la présentation des suites Si*, et de celui qui affiche les valeurs de l'indicatrice, nous constatons, pour les valeurs de x de cet intervalle, que :
    1.    les nombres premiers strictement inférieurs à 13, concernés pour confectionner les dites suites sont : 3, 5, 7 et 11
    2.    φ(3) = 2, φ(5) = 4, φ(7) = 6, φ(11) = 10
           φ(3)φ(5) = 8, φ(3)φ(7) = 12, φ(3)φ(11) = 20, φ(5)φ(7) = 24, φ(5)φ(11) = 40, φ(7)φ(11) = 60
           φ(3)φ(5)φ(7) = 48, φ(3)φ(5)φ(11) = 80, φ(3)φ(7)φ(11) = 120, φ(5)φ(7)φ(11) = 240
           φ(3)φ(5)φ(7)φ(11) = 480

Exemple 1 avec x=121 On a π(x) = π(121) = 30      n = π(x + 2) = π(121 + 2) = 30
S2* = { 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 77, 83, 89, 95, 101, 107, 113, 119 }
S3* = { 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117 }
S4* = { 23, 37, 51, 65, 79, 93, 107, 121 }
S5* = { 35, 57, 79, 101, 123 }
S2* ∩ S3* = { 17, 47, 77, 107 }
S2* ∩ S4* = { 23, 65, 107 }
S2* ∩ S5* = { 35, 101 }
S3* ∩ S4* = { 37, 107 }
S3* ∩ S5* = { 57 }
S4* ∩ S5* = { 79 }
S2* ∩ S3* ∩ S4* = { 107 }
S2* ∩ S3* ∩ S5* = ∅
S2* ∩ S4* ∩ S5* = ∅
S3* ∩ S4* ∩ S5* = ∅
S2* ∩ S3* ∩ S4* ∩ S5* = ∅
Si maintenant nous effectuons les calculs en prenant en compte toutes les suites précédentes, nous obtenons, puisque R(√121 + 2) = R(13) = 3 :
- 3 + (30/2+30/4+30/6+30/10) - (30/8+30/12+30/20+30/24+30/40+30/60) + (30/48+30/80+30/120+30/240) - 30/480
= - 3 + 30 × (1 - 1/2×3/4×5/6×9/10) = -3 + 30 × (1 - 0,28125) = -3 + 30 × 0,71875 = 18,5625 (en application de la note no 3) Et si nous négligeons les quatre derniers termes de cette somme, qui correspondent aux quatre suites vides, nous obtenons :
-3 + (30/2+30/4+30/6+30/10) - (30/8+30/12+30/20+30/24+30/40+30/60) + (30/48) = 17,875 Tandis que G1 a 18 nombres premiers qui sont :  11, 17, 23, 29, 37, 41, 47, 53, 59, 67, 71, 79, 83, 89, 97, 101, 107, 113
Le nombre de sup-jumeaux inférieurs à 121 est donc R(121) = π(121) - (18 + 2) = 30 - (18 + 2) = 10

Exemple 2 avec x=143 On a π(x) = π(143) = 34      n = π(x + 2) = π(143 + 2) = 34
S2* = { 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 77, 83, 89, 95, 101, 107, 113, 119, 125, 131, 137, 143 }
S3* = { 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117, 127, 137 }
S4* = { 23, 37, 51, 65, 79, 93, 107, 121, 135 }
S5* = { 35, 57, 79, 101, 123, 145 }
S2* ∩ S3* = { 17, 47, 77, 107, 137 }
S2* ∩ S4* = { 23, 65, 107 }
S2* ∩ S5* = { 35, 101 }
S3* ∩ S4* = { 37, 107 }
S3* ∩ S5* = { 57 }
S4* ∩ S5* = { 79 }
S2* ∩ S3* ∩ S4* = { 107 }
S2* ∩ S3* ∩ S5* = ∅
S2* ∩ S4* ∩ S5* = ∅
S3* ∩ S4* ∩ S5* = ∅
S2* ∩ S3* ∩ S4* ∩ S5* = ∅
Si maintenant nous effectuons les calculs en prenant en compte toutes les suites précédentes, nous obtenons, puisque R(√143 + 2) = R(13,95) = 3 :
-3 + (34/2+34/4+34/6+34/10) - (34/8+34/12+34/20+34/24+34/40+34/60) + (34/48+34/80+34/120+34/240) - 34/480
= - 3 + 34 × (1 - 1/2×3/4×5/6×9/10) = -3 + 34 × (1 - 0,28125) = -3 + 34 × 0,71875 = 21,4375 (en application de la note no 3) Et si nous négligeons les quatre derniers termes de cette somme, qui correspondent aux quatre suites vides, nous obtenons :
- 3 + (34/2+34/4+34/6+34/10) - (34/8+34/12+34/20+34/24+34/40+34/60) + (34/48) = 20,6583 Tandis que G1 a 21 nombres premiers qui sont :  11, 17, 23, 29, 37, 41, 47, 53, 59, 67, 71, 79, 83, 89, 97, 101, 107, 113, 127, 131, 137
Le nombre de sup-jumeaux inférieurs à 143 est donc R(143) = π(143) - (21 + 2) = 34 - (21 + 2) = 11

Exemple 3 avec x=168 On a π(x) = π(168) = 39      n = π(x + 2) = π(168 + 2) = 39
S2* = { 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71, 77, 83, 89, 95, 101, 107, 113, 119, 125, 131, 137, 143, 149, 155, 161, 167 }
S3* = { 17, 27, 37, 47, 57, 67, 77, 87, 97, 107, 117, 127, 137, 147, 157, 167 }
S4* = { 23, 37, 51, 65, 79, 93, 107, 121, 135, 149, 163 }
S5* = { 35, 57, 79, 101, 123, 145, 167 }
S2* ∩ S3* = { 17, 47, 77, 107, 137, 167 }
S2* ∩ S4* = { 23, 65, 107, 149 }
S2* ∩ S5* = { 35, 101, 167 }
S3* ∩ S4* = { 37, 107 }
S3* ∩ S5* = { 57, 167 }
S4* ∩ S5* = { 79 }
S2* ∩ S3* ∩ S4* = { 107 }
S2* ∩ S3* ∩ S5* = { 167 }
S2* ∩ S4* ∩ S5* = ∅
S3* ∩ S4* ∩ S5* = ∅
S2* ∩ S3* ∩ S4* ∩ S5* = ∅
Si maintenant nous effectuons les calculs en prenant en compte toutes les suites précédentes, nous obtenons, puisque R(√168 + 2) = R(14,96) = 3 :
- 3 + (39/2+39/4+39/6+39/10) - (39/8+39/12+39/20+39/24+39/40+39/60) + (39/48+39/80+39/120+39/240) - 39/480
= - 3 + 39 × (1 - 1/2×3/4×5/6×9/10) = -3 + 39 × (1 - 0,28125) = -3 + 39 × 0,71875 = 25,03125 (en application de la note no 3) Et si nous négligeons les trois derniers termes de cette somme, qui correspondent aux trois suites vides, nous obtenons :
-3 + (39/2+39/4+39/6+39/10) - (39/8+39/12+39/20+39/24+39/40+39/60) + (39/48+39/80) = 24,625 Tandis que G1 a 25 nombres premiers qui sont :  11, 17, 23, 29, 37, 41, 47, 53, 59, 67, 71, 79, 83, 89, 97, 101, 107, 113, 127, 131, 137, 149, 157, 163, 167
Le nombre de sup-jumeaux inférieurs à 168 est donc R(168) = π(168) - (25 + 2) = 39 - (25 + 2) = 12

**********

Quoi qu'il en soit, il est possible de consolider d'une autre manière le point de vue précédent.
Cela consiste à examiner ce qui se passe lorsque l'on fait varier le nombre x de 1000 en 1000 et à comparer les valeurs réelles du cardinal de G1 avec celles que l'on obtient en exécutant le calcul comme il est expliqué plus haut.
On pourrait d'ailleurs, avec des moyens de calcul performants, aller assez loin pour se faire un opinion relativement précise de la situation, en l'absence de preuves rigoureusement établies.
C'est ce qui a été tenté ici jusqu'à x = 15 000 000, les résultats étant donnés dans le tableau ci-dessous assez conséquent.
(Les valeurs placées dans les colonnes nos 6 et 7 sont celles qui servent au calcul des valeurs approchées, colonne 8)



Comme on peut le remarquer, à l'observation des résultats, les écarts sont relativement petits et vont en croissant lentement au fur et à mesure que x augmente, ce qui n'a rien de surprenant.
Cependant, l'erreur commise reste aux environs de 3 pour mille ce qui est peu et même remarquable.
En outre, l'examen de l'avant dernière colonne donne à réfléchir puisque les valeurs calculées pour G1 sont, sauf pour quelques valeurs de x du début du tableau, toujours inférieures aux valeurs réelles (colonne 4), cette constatation pouvant étayer la thèse précédente.
Cela ne veut pas dire pour autant que, pour x très grand, les résultats seront comparables à ceux qui précèdent.


Note no 3

L'opération qui consiste à transformer la somme en un produit comme cela a été fait plus haut :



s'appuie sur des identités élémentaires qui, dans leur plus simple expression, se traduisent par :







et qui se généralisent facilement à un nombre quelconque de naturels non nuls par un raisonnement par récurrence.


Note no 4

Nombre de jumeaux
x103104105106107108109
R(x)3520512248169589804403123424506
x1010101110121013101410151016
R(x)27412679224376048187058522015834664872135780321665117720924230410304195697298



Note no 5

Puisqu'il est établi qu'il y a une infinité de nombres premiers jumeaux, on peut alors se demander s'il est possible d'exprimer R(x+2) pour tout entier x.

L'inégalité ci-dessous, rencontrée au terme de la démonstration du théorème :



entraîne-t-elle, en particulier, la suivante ?



On ne peut l'affirmer en l'absence d'une démonstration, mais on peut le conjecturer.
Toujours est-il qu'ici, un programme informatique approprié serait d'un grand secours et guiderait les recherches dans la bonne direction en utilisant une base de données comportant un nombre important de jumeaux (voir la référence no 15)

Quant au calcul de π(x+2), on peut utiliser la fonction Li(x) à défaut de pouvoir obtenir les valeurs réelles.
Quoi qu'il en soit, l'inégalité précédente est vérifiée pour tout x inférieur à 5.107

A toutes fins utiles, on trouvera en bas de page cinq liens affichant les listes des 970 704 nombres premiers numérotés inférieurs à 15 000 000, et utiles pour la note suivante


Note no 6

Les mêmes moyens peuvent servir pour illustrer le corollaire, bien que ce qu'il énonce soit valable pour des valeurs de x qui tendent vers l'infini.
Cependant, il est tout à fait remarquable que le corollaire soit vérifié pour tout x.

Le tableau suivant montre, grâce à une série de valeurs, comment R(x+2) - R(√x+2) s'écarte de plus en plus de la partie entière de sa borne inférieure π(π(x+2))/1,693034 - 2

x+2√x+2R(x+2)R(√x+2)A = R(x+2) - R(√x+2)π(x+2)π(π(x+2))A - B
103333553016839219
2×1034661655303623421
3×1035681675430824629
4×103651037965501015739
5×1037212671196691216950
6×1037914381357831377857
7×1038516281549001548866
8×10391175816710071689770
9×103961898181111718710873
1041022058197122920111681
2×104143342113312262335195136
3×104175467124553245457267188
4×104202591155764203575337239
5×104225705156905133685402288
6×104246811177946057790464330
7×104266905178886935890523365
8×1042841007199887837990582406
9×104302111619109787131086639458
105318122420120495921184697507
2×10544921602321371798420621215922
3×105549299425296925997285916861283
4×105634380428377633860362621391637
5×105709456530453541538434325631972
6×105776533130530149098504529772324
7×105838606133602856543573633862642
8×105896676635673163951641137842947
9×105950747235743771274705641653272
1061002816935813478498770245473587
2×10614161487146148251489331375281206705
3×106173420932552087721681619349114269451
4×1062002268606126799283146246951458412215
5×1062238324636732396348513298591763414762
6×1062451379167237844412849348332057217272
7×1062647432597443185476648397552347919706
8×1062830486188048538539777445592631722221
9×1063002538678253785602489492902911124674
1073164589808358897664579539113184127056
1,5×10738748366010183559970704763994512438435



Note no 7

nπ(n)li(n)n/ln(n)n / (ln(n) - 1)
1014648
10225302227
103168178145169
1041 2291 2461 0861 218
1059 5929 6308 6869 512
10678 49878 62772 38278 030
107664 579664 918620 421661 459
1085 761 4555 762 2095 428 6815 740 304
10950 847 53450 849 23548 254 94250 701 542
1010455 052 512455 055 615434 294 482454 011 971
101141180548134 118 066 4013 948 131 6544 110 416 301
101236 607 912 01837 607 950 28136 191 206 82537 550 193 650
1013346 065 536 839346 065 645 810334 072 678 387345 618 860 221
10143 204 941 750 8023 204 942 065 6923 102 103 442 166 3 201 414 635 781
101529 844 570 422 66929 844 571 475 28728 952 965 460 21729 816 233 849 001
1016279 238 341 033 925279 238 344 248 557271 434 051 189 532279 007 258 230 820
10172 623 557 157 654 2332 623 557 165 610 8222 554 673 422 960 3052 621 647 966 812 031
101824 739 954 287 740 86024 739 954 309 690 41524 127 471 216 847 32424 723 998 785 919 976
1019234 057 667 276 344 607234 057 667 376 222 382228 576 043 106 974 646233 922 961 602 470 391
10202 220 819 602 560 918 8402 220 819 602 783 663 4832 171 472 409 516 259 1382 219 671 974 013 732 243
102121 127 269 486 018 731 92821 127 269 486 616 126 18220 680 689 614 440 563 22121 117 412 262 909 985 552
1022201 467 286 689 315 906 290201 467 286 691 248 261 498197 406 582 683 296 285 296201 381 995 844 659 893 518
10231 925 320 391 606 803 968 9231 925 320 391 614 054 155 1391 888 236 877 840 225 337 6141 924 577 459 166 813 514 800
102418 435 599 767 349 200 867 86618 435 599 767 366 347 775 14418 095 603 412 635 492 818 79718 429 088 896 563 917 716 963
1025176 846 309 399 143 769 411 680176 846 309 399 198 930 392 619173 717 792 761 300 731 060 452176 788 931 049 963 678 496 486
10261 699 246 750 872 437 141 327 6031 699 246 750 872 593 033 005 7241 670 363 391 935 583 952 504 3421 698 738 497 929 718 386 117 081
102716 352 460 426 841 680 446 427 39916 352 460 426 842 189 113 085 40516 084 980 811 231 549 172 264 03416 347 937 065 228 978 294 751 933



Note no 8

Valeur de la constante d'Euler-Mascheroni (10 000 décimales) :

γ = 0.
5772156649 0153286060 6512090082 4024310421 5933593992 3598805767 2348848677 2677766467 0936947063 2917467495 1463144724 9807082480 9605040144 8654283622 4173997644 9235362535 0033374293 7337737673 9427925952 5824709491 6008735203 9481656708 5323315177 6611528621 1995015079 8479374508 5705740029 9213547861 4669402960 4325421519 0587755352 6733139925 4012967420 5137541395 4911168510 2807984234 8775872050 3843109399 7361372553 0608893312 6760017247 9537836759 2713515772 2610273492 9139407984 3010341777 1778088154 9570661075 0101619166 3340152278 9358679654 9725203621 2879226555 9536696281 7638879272 6801324310 1047650596 3703947394 9576389065 7296792960 1009015125 1959509222 4350140934 9871228247 9497471956 4697631850 6676129063 8110518241 9744486783 6380861749 4551698927 9230187739 1072945781 5543160050 0218284409 6053772434 2032854783 6701517739 4398700302 3703395183 2869000155 8193988042 7074115422 2781971652 3011073565 8339673487 1765049194 1812300040 6546931429 9929777956 9303100503 0863034185 6980323108 3691640025 8929708909 8548682577 7364288253 9549258736 2959613329 8574739302 3734388470 7037028441 2920166417 8502487333 7908056275 4998434590 7616431671 0314671072 2370021810 7450444186 6475913480 3669025532 4586254422 2534518138 7912434573 5013612977 8227828814 8945909863 8460062931 6947188714 9587525492 3664935204 7324364109 7268276160 8775950880 9512620840 4544477992 2991572482 9251625127 8427659657 0832146102 9821461795 1957959095 9227042089 8962797125 5363217948 8737642106 6060706598 2561990102 8807561251 9913751167 8217643619 0570584407 8357350158 0056077457 9342131449 8850078641 5171615194 5657061704 3245075008 1687052307 8909370461 4306684817 9164968425 4915049672 4312183783 8753564894 9508684541 0234060162 2508515583 8672349441 8788044094 0770106883 7951113078 7202342639 5226920971 6088569083 8251137871 2836820491 1789259447 8486199118 5293910293 0990592552 6691727446 8920443869 7111471745 7157457320 3935209122 3160850868 2755889010 9451681181 0168749754 7096936667 1210206304 8271658950 4932731486 0874940207 0067425909 1824875962 1373842311 4426531350 2923031751 7225722162 8324883811 2458957438 6239870375 7662855130 3314392999 5401853134 1415862127 8864807611 0030152119 6578006811 7773763501 6818389733 8966398689 5793299145 6388644310 3706080781 7448995795 8324579418 9620260498 4104392250 7860460362 5277260229 1968299586 0988339013 7871714226 9178838195 2984456079 1605197279 7360475910 2510995779 1335157917 7225150254 9293246325 0287476779 4842158405 0759929040 1855764599 0186269267 7643726605 7117681336 5590881554 8107470000 6233637252 8894955463 6971433012 0079130855 5263959549 7823023144 0391497404 9474682594 7320846185 2460587766 9488287953 0104063491 7229218580 0870677069 0427926743 2844469685 1497182567 8095841654 4918514575 3319640633 1199373821 5734508749 8832556088 8873528019 0191550896 8855468259 2454445277 2817305730 1080606177 0113637731 8246292466 0081277162 1018677446 8495951428 1790145111 9489342288 3448253075 3118701860 9761224623 1767497755 6412461983 8564014841 2358717724 9554224820 1615176579 9408062968 3424289057 2594739269 6386338387 4380547131 9676429268 3724907608 7507378528 3702304686 5034905120 3422721743 6689792848 6297290889 2678977703 2624623912 2618887653 0057786274 3606094443 6039280977 0813383693 4235508583 9411267092 1873441451 2187803276 1505094780 5546630058 6845563152 4546053151 1325281889 1079231491 3110323443 0245093345 0003076558 6487422297 1770033178 4539150566 9401599884 9291609114 0029486902 0884853816 9700955156 6347055445 2217640358 6293982865 8131238701 3253588006 2568662692 6997767737 7306832269 0091608510 4515002261 0718025546 5928493894 9277595897 5407615599 3378264824 1979506418 6814378817 1850885408 0367996314 2395400919 6438875007 8900000627 9979428098 8637299259 1977765040 4099220379 4042761681 7837156686 5306693983 0916524322 7059553041 7667366401 1679295901 2930537449 7183080042 7584863508 3808042466 7350935598 3232411696 9214860649 8927636244 3295885487 3789701489 7133435384 4800289046 6650902845 3768962239 8304881406 2730540879 5911896705 7493854432 4786914808 5337702640 6775808127 5458731117 6364787874 3073920664 2011251352 7274996175 4505308558 2356683068 3229176766 7704103523 1535032510 1246563861 5670644984 7132695969 3301678661 3833333344 1657900605 8674971036 4689517456 9597181553 7640783776 5018427834 5991842015 9954314490 4772555230 6147670165 9934163906 6091205400 5322158902 0913408027 8225153385 2899511665 4522458691 8599367122 0132150144 8014242309 8625460448 8672569343 1488704915 9304464018 9164502022 4054953862 9184758629 3077889350 6437715966 0690960468 1243702305 4657031606 7999258716 6675247219 4097779801 8636262563 3582526279 4223932548 6013269353 0701388937 4369238428 7893851276 4740856548 6502815630 6774044220 3064403756 8263091029 1751457223 4441050369 3177114521 7088890744 6416048688 7010838623 1142612844 1425960956 3704006192 0057933503 4155242624 0262064656 9354306125 8526583452 1921214977 7187806958 6608516334 9221048367 3799459259 4340379560 0021927854 1837941776 0203365594 6730788798 3808481631 4678241492 3546491488 7668336840 7492893865 2818630485 8982035481 8624383848 1759976358 4907518079 1480634943 9162847054 8220075494 5348986133 8272357309 2219003074 0096800337 6668449325 0556765493 7530318112 5164105524 9238407764 5149842395 7620127815 5232294492 8854557853 8202489189 4244185709 5919558208 1000715783 8403962747 9985817880 8888657168 3069943606 0735990421 0685114279 1316969959 6792300828 9881560975 3833805910 9360341252 9986567903 8956879567 3455083362 9078238626 3856349074 7319275278 7401665575 3119011154 3470018186 2569712611 2012685292 3129937161 4039069651 1222481661 5082353643 9823966205 3263332224 8505191593 6826907150 0431558987 1802783353 8454483091 0724949805 7880961717 9963371670 3655418004 1464667538 7195869484 8333154358 3330641935 9294874209 5147883234 7748481418 1497768716 9441364005 6645156936 1165241615 5573414193 5424721373 0674683338 4905442662 6038372788 2175527099 3095814102 6136979500 7864658767 7160863080 4460749802 8015769626 7591389779 4772214337 5154708293 4587912389 8433055067 2234749699 8494248670 6721502569 2735295850 6586958899 7486535562 1869580439 9712516897 6654169862 6538628919 7754218772 1939605817 0011042364 1415878081 0386172101 5575519237 1116004988 0682291618 0977324219 5832897486 9227183979 1904677165 4266813889 3379296036 8154579396 1133962192 2245430151 5806317437 0840560853 6416031384 9829695185 6695261282 2123716939 3681303212 9656193971 8710207098 0079488339 1019753510 4307441823 4488333317 9697827733 2091143324 5143050865 7345750068 7391475470 7775775599 1846711830 8583660159 4371937184 4903906177 0232536567 9775967444 7574751158 4195746700 9973450024 5442840658 5024508585 6463927912 4611987909 3693072019 8040293036 0373883843 0742162821 2016353864 6622609719 8958436799 4305720301 4963805083 2232365825 5577245342 3718773743 9818333306 4546629069 9331112597 3721950274 6468990654 5715544030 3917835419 7564343157 3903488386 6750542742 1618310500 6055046422 3545708427 3935493590 5176271747 9299472398 9086329701 0190561010 7742690926 4752357403 0463015924 3442464900 8341886308 5932068552 2507790910 1958588953 1432879981 7570981916 8293159404 5300563254 3314488517 3573026982 5693725346 9964013440 8715801081 4528786579 0408663637 9450711085 0510424179 7691911292 6151320103 1636349808 6606948624 4078006684 0067169622 1463718114 7772683418 4664636424 2734053003 1380773496 1199814686 1768585463 1208163164 7989379642 6373835661 8938313710 9832895649 0521148813 4029742388 8686315431 3297876579 9125454243 3385634720 0268129048 9949550426 9808821302 6726358153 2480675387 9032305742 1040330149 7887867523 7786070546 8861472100 9926329425 1088780197 0284117922 4025910914 6658480925 7857192786 2821476670 7408786351 9714256292 4278670284 0770324143 7569931883 2433315590 0243330476 9111009247 9791180062 8620221370 7800621725 7329047359 9439888313 9279927969 3970635676 2811669405 4128859081 9820238382 7703548349 6879734048 8882930167 3677094158 4654400954 8624651461 0135391349 6855912040 2363618721 5099298065 1905861682 8153028750 4275452586 0533196343 2595777478 8134372393 9499124380 6143754498 5906860751 8563142725 5255642593 9670149804 1425981823 7852576829 4363959656 2438852065 6548071038 8454639445 3770191784 5718741011 8622322780 2525194362 6574382422 5609356769 2582387749 1160737759 4514014470 3190224153 5591125061 3817829742 1264982641 6187246063 1334089192 6702359795 8023658416 3175567923 3566210123 1335845494 5905900699 8420067226 0251167743 8473648243 8571540714 6265945642 3911271707 8030637141 6926386440 1005713109 5896063264 9637552956 7693646894 1051795200 0616452021 8843534047 3018243930 5148819845 9307629640 4445687762 4165287162 0727673186 0632540801 4288745711 9865730747 1701886603 6879703647 7085485287 1670003622 9285288374 6824660588 1411754047 4460616763 5430373992 3756596593 6967087923 1677446856 9310838210 7830483159 1964300214 4125970228 9063203174 1011493664 8095290301 1716334531 9179229392 4242877283 7872349569 9292321360 9223494722 6458243755 0945153355 2011761289 7517339513 7178293328 7158609438 6627011791 8415545872 6489825139 2555943795 1973178674 4876992532 6179423381 2999412793 9860264424 5196006054 3681866467 0986594436 5930154376 2914869795 9769499653 3527210020 0209679104 3948254724 4113342244 8700546376 5684086676 2153373627 4615912054 7008629057 1698257353 7052397612 3123841256 4349411789 4986158285 9702097109 7039196352 1681225822 4756271951 9382728285 2091471823 7534365525 4020746203 0667304769 5247009441 3814561782 8266631961 3967359367 2572646033 8849464248 9472448978 4815967153 0615384671 2236987128 2319784769 3110571662 3637326207 5959711804 0151438962 3170601958 5709823813 9246661352 7913695637 6559048616 7620512974 0998314965 5978602534 1012945439 9867288300 6244084401 8618151175 0687088764 6716097992 9201776962 4963301575 8292596188 4948587200 2292248060 6288121778 7338314588 2551293953 6510881918 6512004492 3154983947 7314735786 8897314204 7310945381 4648226321 0233107943 9597462852 3541295751 9106355879 2300195618 1312946120 3015757634 0159785681 7517498423 7788244737 5398247457 5996867707 4085455743 2942402678 1938482203 5409621060 6072192499 0825104854 0031849631 9986322156 9089097614 0531071651 1312932685 3498524402 8644829347 0591608586 9959819889 0395995591 8110764134 4665881452 5425658815 3545028884 7399753243 2780902152 2569521844 1452986508 3551298398 0226238264 9748818115 8152503459 9749915966 4009832014 5200704803 5556858997 3099815031 0419223850 8974537327 6129471712 6816530886 7005472886 5779224670 1782659482 7260972290 3471574140 3166973107 0505078296 1082607287 0429126082 3119741510 1473578478 1010727971 1242797602 8481411516 3388689690 7867175772 5938152479 6123789999 0366617560 3588218132 5467563448 3091487296 2669372198 8502700188 2981730170 2494421406 3172651971 3950622108 2764507181 6639104366 8329566380 7307194543 2112550536 2089678323 0310851714 8114928588 9936287064 8875584389 1300471868 4679858165

Valeur de la constante de Shah et Wilson :
C2 = 0.6601618158 4686957392 7812110014 5557784326 2336028473 3413319448 4233354056 4230449527 7143760031 4138398679 11779 ...


Note no 9

Il existe un critère simple, mais inutilisable pour de grands nombres, permettant de dire si deux nombres n et n+2 sont des nombres premiers (donc jumeaux).
Ce critère est exposé ci-dessous.

Proposition

Si n est un entier strictement supérieur à 1 alors les énoncés suivants sont équivalents :
A) n et n+2 sont deux nombres premiers
B) 4 × [(n-1)! + 1] + n ≡ 0 mod[n(n+2)]    (0)    

Preuve

1)    A ⇒ B

n+2 étant premier, on a, d'après le théorême de Wilson (n+1)! + 1 ≡ 0 mod(n+2)    (I)
Or n ≡ -2 mod(n+2) et n+1 ≡ -1 mod(n+2)    donc n × (n+1) ≡ 2 mod(n+2)
On en déduit que
(n+1)! + 1 = (n-1)! × n × (n+1) + 1 ≡ 2 × (n-1)! + 1 mod(n+2)     (II)
On tire alors de     (I)     et     (II)     :    2 × (n-1)! + 1 ≡ 0 mod(n+2)
Il existe donc un entier p tel que 2 × (n-1)! + 1 = p(n+2) = pn + 2p     (III)
D'où il résulte que 2 × (n-1)! + 1 ≡ 2p mod(n)     (IV)
Mais, n étant premier, on a aussi : (n-1)! + 1 ≡ 0 mod(n)
ce qui s'écrit encore : (n-1)! ≡ -1 mod(n)    ou    2 × (n-1)! ≡ -2 mod(n)    ou    2 × (n-1)! + 1 ≡ -1 mod(n)     (V)
On tire alors de     (IV)     et     (V)     :    -1 ≡ 2p mod(n)
Il existe donc un entier q tel que 2p = -1 + qn
Mais, de     (III)     on tire : 4 × (n-1)! + 2 = 2p(n+2) = (-1 + qn)(n+2) = - n - 2 + qn(n+2)
Egalité qui permet d'écrire : 4 × (n-1)! + 4 + n = qn(n+2), c'est-à-dire : 4 × [(n-1)! + 1] + n ≡ 0 mod[n(n+2)]    C.Q.F.D.

2)    B ⇒ A

L'hypothèse 4 × [(n-1)! + 1] + n ≡ 0 mod[n(n+2)]     (0)    implique qu'il existe un entier p tel que 4 × (n-1)! + 4 + n = pn(n+2)     (VI)
Cela dit, nous allons montrer par l'absurde que n est impair.
Supposons donc que n est pair, et donc que n+2 l'est également.
Alors l'un de ces deux nombres pairs consécutifs est forcément un multiple de 4 et deux cas se présentent alors.

1er cas        n est multiple de 4.
Dans ce cas, il existe un entier q tel que n = 4q (q<n)
L'égalité     (VI)     devient alors 4 × (n-1)! + 4 + 4q = p × 4q × (n+2), c'est-à-dire (n-1)! + 1 + q = pq(n+2)
q divise donc le premier membre de cette égalité et donc aussi (n-1)! + 1
Mais q divise aussi (n-1)! car q<n, et donc aussi la différence [(n-1)! + 1] - (n-1)! c'est-à-dire 1
On a donc q=1 et donc n=4 ce qui est impossible puisqu'autrement on aurait, d'après     (0)     4 × [(4-1)! + 1] + 4 = 32 ≡ 0 mod[4(4+2)] ce qui est absurde
n ne peut donc être un multiple de 4 et ce cas est à rejeter.

2ième cas        n+2 est multiple de 4.
Dans ce cas, il existe un entier q tel que n+2 = 4q, ce qui s'écrit encore n ≡ -2 mod(4)
Dès lors, de     (VI)     on tire : n = pn × (4q) - 4 × (n-1)! - 4 = 4 × [pnq - (n-1)! - 1] ≡ 0 mod(4)
On a donc 0 ≡ -2 mod(4) ce qui est absurde
n+2 ne peut donc être un multiple de 4 et ce cas est à rejeter.

Il résulte donc de ce qui précède que n est impair

Ce point étant acquis, l'hypothèse 4 × [(n-1)! + 1] + n ≡ 0 mod[n(n+2)]    (0)    implique évidemment 2 × [2 × (n-1)!] + (4 + n) ≡ 0 mod(n+2)     (VII)
L'hypothèse 4 × [(n-1)! + 1] + n ≡ 0 mod[n(n+2)]    (0)    implique 4 × [(n-1)! + 1] ≡ 0 mod(n)
n étant impair et donc premier avec 4 divise donc (n-1)! + 1, ce qui signifie que n est premier d'après le théorème de Wilson.    C.Q.F.D.
Par ailleurs, on a d'une part 2 × (n-1)! ≡ (n+1)! mod(n+2)    (voir II)    et d'autre part 4 + n ≡ 2 mod(n+2)
Cela entraîne, en considérant     (VII)     2 × (n+1)! + 2 ≡ 0 mod(n+2)    ou    2 × [(n+1)!+ 1] ≡ 0 mod(n+2)
n+2 étant impair et donc premier avec 2 divise donc (n+1)! + 1, ce qui signifie que n+2 est premier d'après le théorème de Wilson.    C.Q.F.D.

Exemple

Nous savons que les entiers n=29 et n+2=31 sont des premiers jumeaux. Appliquons leur le critère précédent.
Il s'agit de vérifier que 4 × [28! + 1] + 29 ≡ 0 mod(29 × 31)
Ou que 4 × [304 888 344 611 713 860 501 504 000 000 + 1] + 29 ≡ 0 mod(899)
Ou que 4 × 304 888 344 611 713 860 501 504 000 001 + 29 est divisible par 899.
Ou que 1 219 553 378 446 855 442 006 016 000 003 est divisible par 899.
Le quotient est en effet l'entier 1 356 566 605 613 854 774 200 240 267.


Références

1.      Crible de Sundaram

2.      Th&eacut!×n×(n+1) + 1 ≡ 2(n-1)! 1 mod(n+2) sion_exclusion_principle" title="http://www.en.wikipedia.org/wiki/Inclusion_exclusion_principle">Crible de Poincarré

4.      Troisième théorème de Mertens

5.      Constante d'Euler-Mascheroni

6.      Constante de Shah et Wilson

7.      Comportement asymptotique de la fonction π(n).ln(n) / n

8.      Première conjecture de Hardy-Littlewood

9.      Les 10 000 premières décimales de la constante d'Euler-Mascheroni

Ci-dessous une base de données formée de gros fichiers. Firefox est le navigateur le plus approprié pour effectuer les chargements.

----- Les nombres premiers numérotés -----

10.      de 2 à 3 000 000

11.      de 3 000 000 à 6 000 000

12.      de 6 000 000 à 9 000 000

13.      de 9 000 000 à 12 000 000

14.      de 12 000 000 à 15 000 000

----- Les sup-jumeaux numérotés -----

15.      de 5 à 100 000 000

16.      de 100 000 000 à 200 000 000

17.      de 200 000 000 à 300 000 000

18.      de 300 000 000 à 400 000 000

19.      de 400 000 000 à 500 000 000

20.      de 500 000 000 à 600 000 000

21.      de 600 000 000 à 700 000 000

22.      de 700 000 000 à 800 000 000

23.      de 800 000 000 à 900 000 000

24.      de 900 000 000 à 1 000 000 000

25.      de 1 000 000 000 à 1 100 000 000

26.      de 1 100 000 000 à 1 200 000 000

27.      de 1 200 000 000 à 1 300 000 000

28.      de 1 300 000 000 à 1 400 000 000

29.      de 1 400 000 000 à 1 500 000 000

30.      de 1 500 000 000 à 1 600 000 000

31.      de 1 600 000 000 à 1 700 000 000

32.      de 1 700 000 000 à 1 800 000 000

33.      de 1 800 000 000 à 1 900 000 000

34.      de 1 900 000 000 à 2 000 000 000